This is a basic arithmetic quiz that will test your knowledge about the signs of trigonometric functions in the four quadrants Quandrant 1 0˚ θ 90˚, Quandrant 2 90˚ θ 180˚, Quandrant 3 180˚ θ 270˚, Quandrant 4 270˚ θ 360˚Do you know the signs of these trigonometric functions Sine, Cosine, Tangent, Secant, Cosecant, and Cotangent in these quandrantsPreCalculus – NJCTLTrigonometric Functions ~1~org PRECALCULUS UNIT 4 TRIGONOMETRY PRACTICE PROBLEMS Angle and Radian Measures Convert each degree measure into radians Round answers to the 4th decimal place 1 ° 2 ° 3 ° Convert each radian measure into degrees Round answers to the 4th decimal place 4 025Trigonometry Find the Other Trig Values in Quadrant III sin (theta)=2/3 sin(θ) = 2 3 sin ( θ) = − 2 3 Use the definition of sine to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the values sin(θ) = opposite hypotenuse sin ( θ) = opposite hypotenuse

Chapter 6 Trigonometry Section 6 4 Trigonometric Functions
Quadrant 1 2 3 4 trigonometry
Quadrant 1 2 3 4 trigonometry-Section 43 Trigonometric Functions of Angles Unit Circle Trigonometry An angle is in standard position if its vertex is at the origin and its initial side is along the positive x axis Positive angles are measured counterclockwise from the initial side Negative angles are measured clockwise We will typically use the T to denote an angle0611 · Quadrant I (angles from 0 to 90 degrees, or 0 to π/2 radians) All trigonometric functions are positive in this quadrant Quadrant II (angles from 90 to 180 degrees, or π/2 to π radians) Sine and cosecant functions are positive in this quadrant Quadrant III (angles from 180 to 270 degrees, or π to 3π/2 radians) Tangent and cotangent functions are positive in this quadrant Quadrant IV (angles from 270 to 360 degrees, or 3π/2
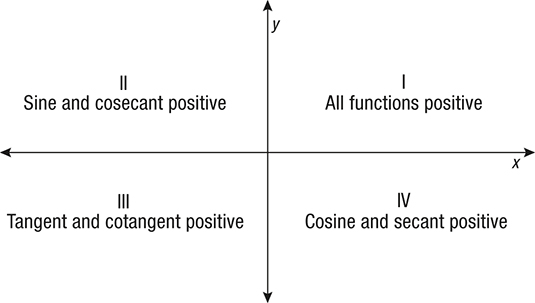


What Trig Functions Are Positive In Which Quadrants Socratic
Trigonometry Examples Popular Problems Trigonometry Find the Other Trig Values in Quadrant II tan(0)=(3/4) Use the definition of tangent to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the valuesMath Cheat Sheet for Trigonometry One Time Payment $1299 USD for 2 months Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year untilNamaste to all Friends, This Video Lecture Series presented By VEDAM Institute of Mathematics is Useful to all student
And use "&" or "and", not "plus" or "" In which quadrant is / are the point(s) ( x , y ) , such that xy < 0 ?Students can download 11th Business Maths Chapter 4 Trigonometry Ex 41 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 412218 · sin(α β) = sin α cos β cos α sin βsin(α − β) = sin α cos β − cos α sin βThe cosine of the sum and difference of two angles is as follows cos(α β) = cos α cos β − sin α sin βcos(α − β) = cos α cos β sin α sin βProofs of the Sine and Cosine of the Sums and Differences of Two Angles We can prove these identities in a variety of ways
Answer Key Testname TRIGONOMETRY 62 SHORT VERSION 1) 3 2 2) " = 175°, # = 55° 3) cos !1609 · Students can download 11th Business Maths Chapter 4 Trigonometry Ex 42 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 42Trigonometry Examples Popular Problems Trigonometry Find the Other Trig Values in Quadrant III tan The quadrant determines the sign on each of the values Find the hypotenuse of the unit circle triangle Since the opposite and adjacent sides are known, use the Pythagorean theorem to find the remaining side Replace the known values in


The Trigonometric Ratios Of Angl



42 Printable Unit Circle Charts Diagrams Sin Cos Tan Cot Etc
This is a basic arithmetic quiz that will test your knowledge about the signs of trigonometric functions in the four quadrants Quandrant 1 0˚ θ 90˚, Quandrant 2 90˚ θ 180˚, Quandrant 3 180˚ θ 270˚, Quandrant 4 270˚ θ 360˚Do you know the signs of these trigonometric functions Sine, Cosine, Tangent, Secant, Cosecant, and Cotangent in these quandrantsTrigonometric Circle Used To Convert The Angles From Quadrants 2 3 And Download Scientific Diagram Save Image Astc Formula Save Image Content The Four Quadrants Save Image Trigonometry With Any Angle S Cool The Revision Website Save Image Higher Maths 1 2 3 Trigonometric Functions Save Image 5 Signs Of The Trigonometric FunctionsTrigonometry 9 23 Sign variation for the trigonometric numbers by quadrant Inside a quadrant the trigonometric numbers keep the same sign (fig 6) sine cosecant cosine secant tangent cotangent fig6 sign variation for the trigonometric numbers by quadrant 24 Pythagorean identities



Trigonometric Circle Used To Convert The Angles From Quadrants 2 3 And Download Scientific Diagram



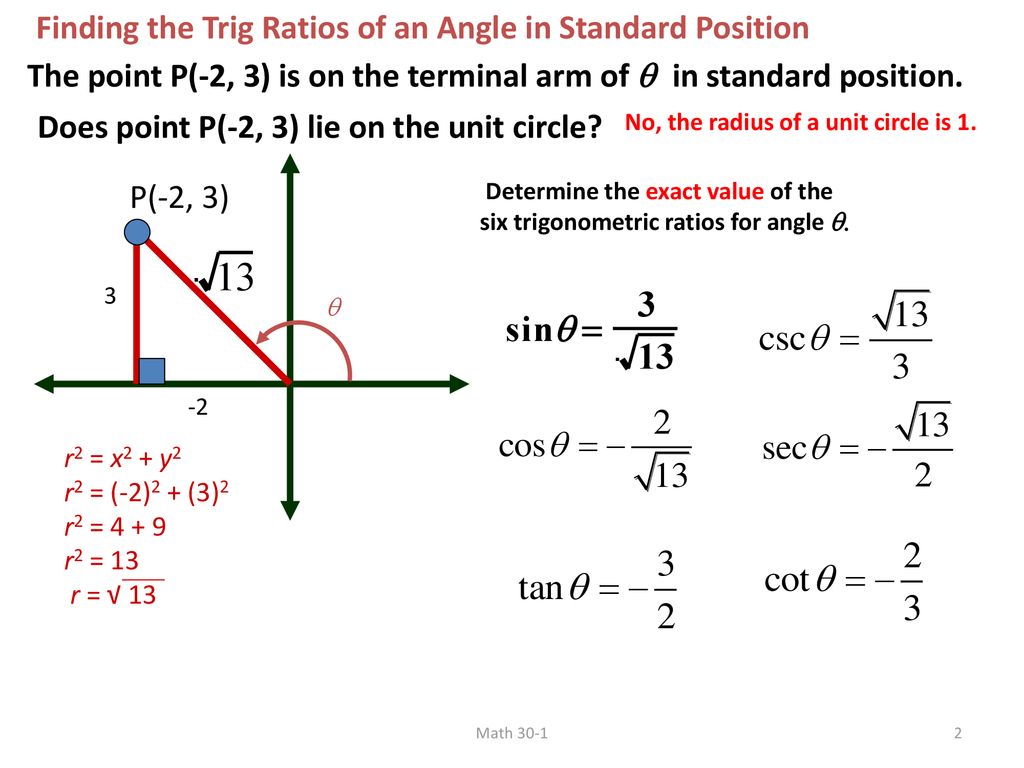
Solved 44 Sec 8 45 Sec 8 40 Csc 8 Sin 8 Tan 8 Cot Chegg Com
The values for this process are given below \sin 33^ {\circ} \approx \sin 327^ {\circ} \approx \cos 33^ {\circ} \approx 087 \cos 327^ {\circ} \approx 087 \tan 33^ {\circ} \approx \quad \tan 327^ {\circ} \approx In Quadrant I, ALL the trigonometric functions are positiveInverse Trig Function Quadrants, Inverse Trig Function Formulas, Trig Quadrant Chart, Unit Circle with Trig Functions, Inverse Trig Function Ranges, Inverse Trig Triangles, Quadrants Sin Cos Tan, Inverse Sine Function, Inverse Cosine Function, Trigonometric Functions Quadrants, Inverse Trig Graphs, Inverse Tangent Function, Unit Circle Quadrant 1, Inverse Trig Functions Table, InverseUse of calculator to Find the Quadrant of an Angle 1 Enter the angle in Degrees top input example 1250 in Radians second input as a fraction of π Example 27/5 π or 12 π then press the button "Find Quadrant" on the same row If you enter a quadrantal angle, the axis is displayed Example "negative y axis"
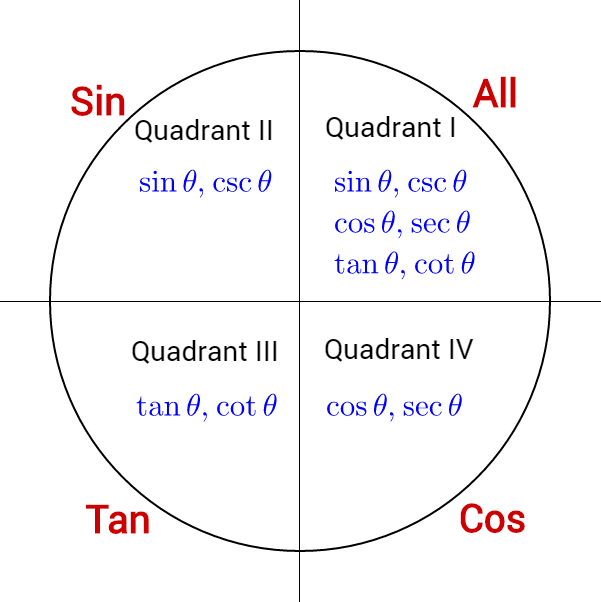


4 05 Trigonometric Functions Of Any Angle


Quadrant
Quadrant System in Trigonometry JEE Main Maths JEE Main 21 Learn Trigonometry Quadrant Rule & Trigonometry Quadrant Formula Class 11 with Neha Ma'amUse Roman "I, II, III, IV", not Arabic "1, 2, 3, 4";Evaluate 6 trig function values x = 1/3 and the radius of unit circle is 1, therefor cos x = 1/3 > x = 70^@53 (Quadrant IV) sin^2 x = 1 cos^2 x = 1 1/9 = 8/9 > sin x = (2sqrt2)/3 Since arc x is in Quadrant IV, then sin x = sqrt2/3 tan x = sin x/(cos x) = (sqrt2/3)(3/1) = sqrt2 cot x = 1/(tan x) = 1/sqrt2 = sqrt2/2 sec x = 1/(cos x) = 3 csc x = 1/(sin x) = 3/(2sqrt2



Trigonometry
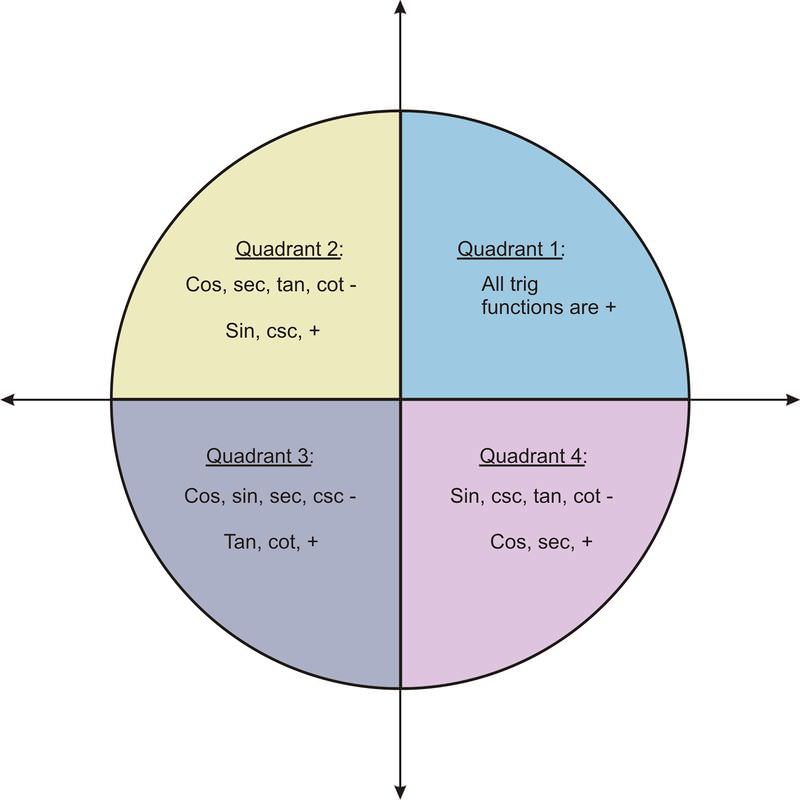


Domain Range And Signs Of Trigonometric Functions Read Trigonometry Ck 12 Foundation
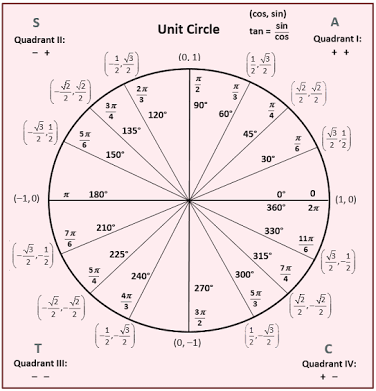
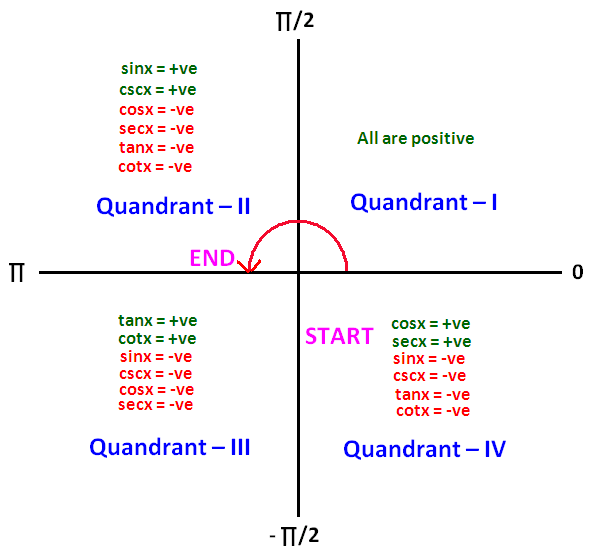
Step 1 Since θ \theta θ is greater than 270°, we are now based in quadrant 4 Step 2 Recall that secant is the reciprocal of cosine Going back to our memory aid, specifically the fourth letter in our acronym, ASTC, we see that cosine is positive in quadrant 4 Step 3 In quadrant four, sine, tangent and their reciprocals are negativeStart studying Trigonometry Quiz Quadrants 1,2,3,4 Learn vocabulary, terms, and more with flashcards, games, and other study toolsThe values of sin, cos, tan, cot at the angles of 0°, 30°, 60°, 90°, 1°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°
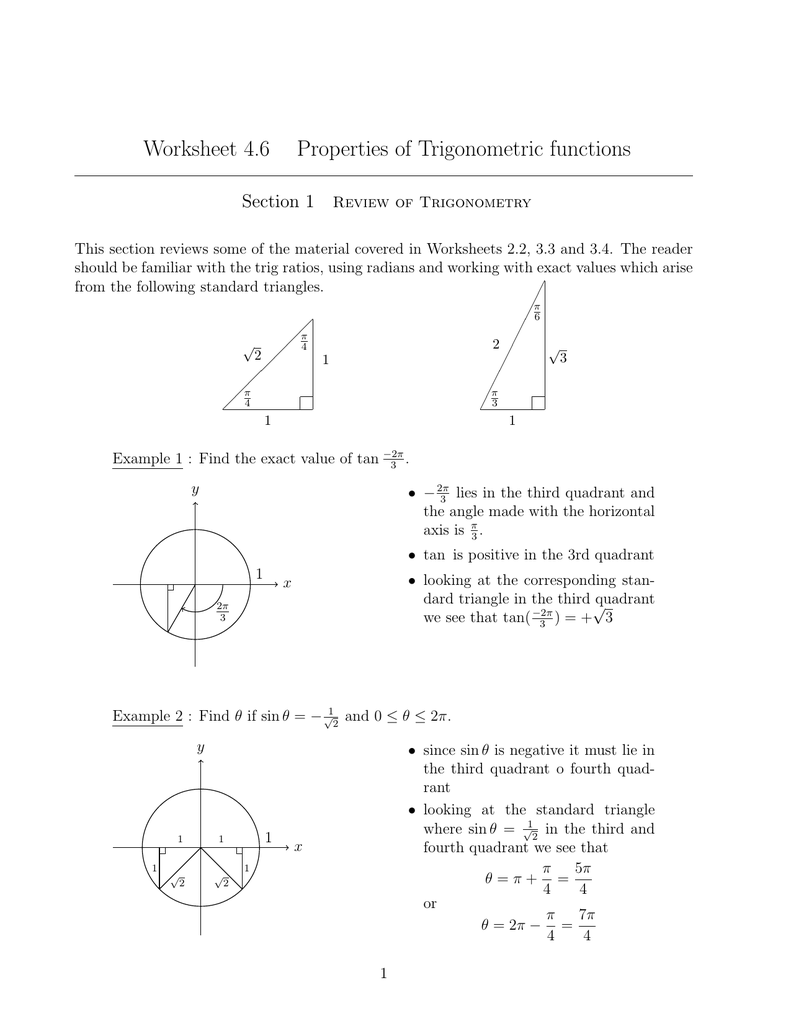


Worksheet 4 6 Properties Of Trigonometric Functions
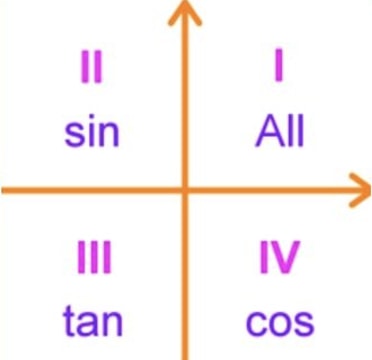


What Is All Students Take Calculus In Trig Studypug
4 and 3 in conjunction with the CAST rule to determine the value and the sign J GarvinExact Values of Trigonometric Ratios Slide 6/16 Using the 12p 3 triangle, the opposite side to 3 has a length of pLearn trigonometry 2 values quadrant with free interactive flashcards Choose from 135 different sets of trigonometry 2 values quadrant flashcards on Quizlet6 4) 1 2 5) cot " cot # 1 6) 1 2 ( 3 cos x sin x) 7)14 24 21
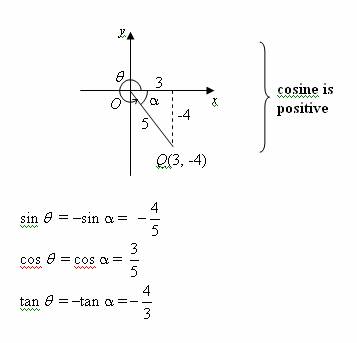


Trigonometric Ratios Solutions Examples Videos
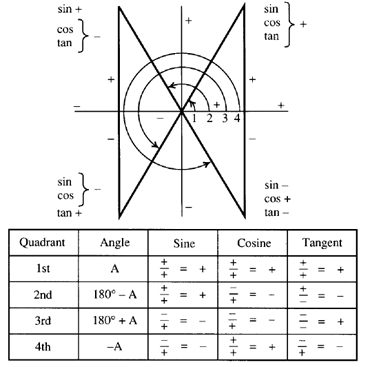


Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
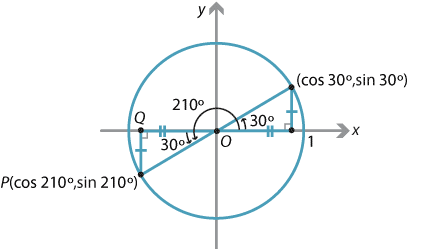
Wwwmath30ca Trigonometry LESSON TWO The Unit Circle Lesson Notes a) A circle centered at the origin can be represented by the relation x2 y2 = r2, where r is the radius of the circle Draw each circle i x2 y2 = 4 ii x2 y2 = 49 Example 1 Introduction to Circle Equations (cos f, sin f)1010 1010 1010 10 10 b) A circle centered at the origin with a radius of 1 has theAn angle is in standard position when its vertex is at the origin, its initial side is on the positive xaxis, and the terminal side rotates counterclockwise from the initial side The position of the terminal side determines the sign of the various trig functions of that angle The following shows you which functions are · The lower part is 1/3rd of the whole length At a point in the horizontal plane through the base of the pole and meters away, the upper part of the pole subtends an angle whose tangent is 1/2 Calculate the possible heights of the pole 6 Solve the equation tan1 3x tan1 2x = π/4 7 Calculate the value tan1 √6 – sec1 (–3) 8



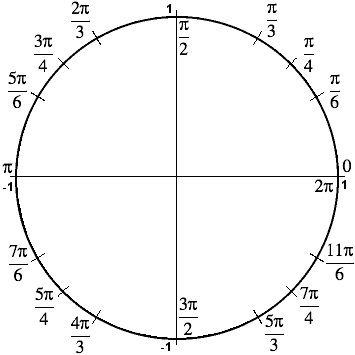
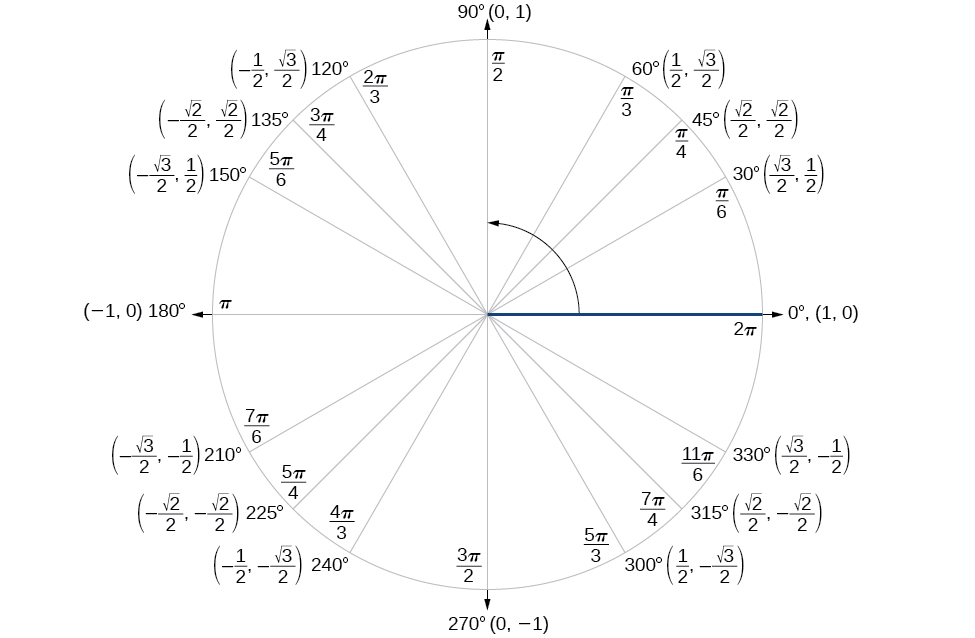
Unit Circle


Unit Circle Trigonometry
Maths Tutorial Trigonometry Law of Sines / Sine Rule Duration 953 Further Maths 1,081,605 views 953 Trigonometry Four Quadrants (Additional Mathematics Secondary 3/4)Trigonometry Find the Other Trig Values in Quadrant I cos (s)=3/4 cos (s) = 3 4 cos ( s) = 3 4 Use the definition of cosine to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the values cos(s) = adjacent hypotenuse cos (More resources available at wwwmisterwootubecom
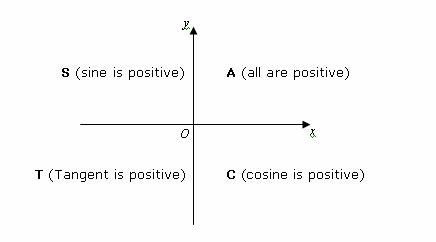


Trigonometric Ratios Solutions Examples Videos


Content The Four Quadrants
Trigonometry 1TRIGONOMETRIC RATIOS 1 0o π/6 π/4 π/3 π/2 sec 1 2/ 3 2 2 undefined cosec undefined 2 2 2/ 3 1 cot undefined 3 1 1/ 3 0 tan 0 1/ 3 1 3 undefined cos 1 3/2 1/ 2 1/2 0 1 3, find cos θ and determine the quadrant in which · Summary First Quadrant All are positive in this quadrant Second Quadrant Only sin is positive in this quadrant Third Quadrant Only tan is positive in this quadrant Fourth Quadrant Only cos is positive in this quadrant We now consider angles in cartesian planeLearn algebra ii trigonometry values quadrant with free interactive flashcards Choose from 500 different sets of algebra ii trigonometry values quadrant flashcards on Quizlet


Trigonometry Facts The Amazing Unit Circle


7 2 Sum And Difference Identities Mathematics Libretexts
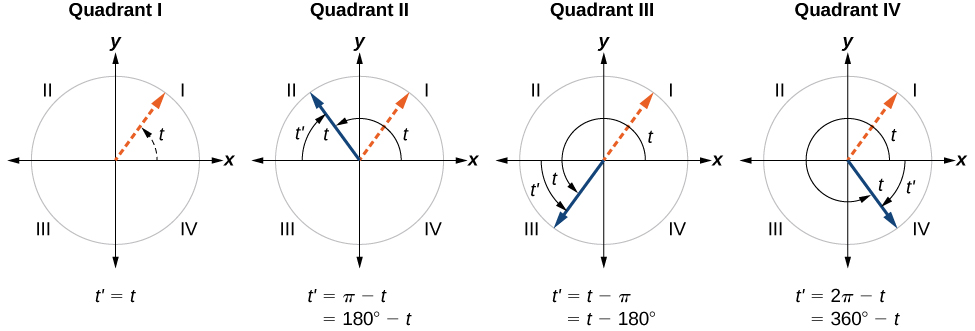
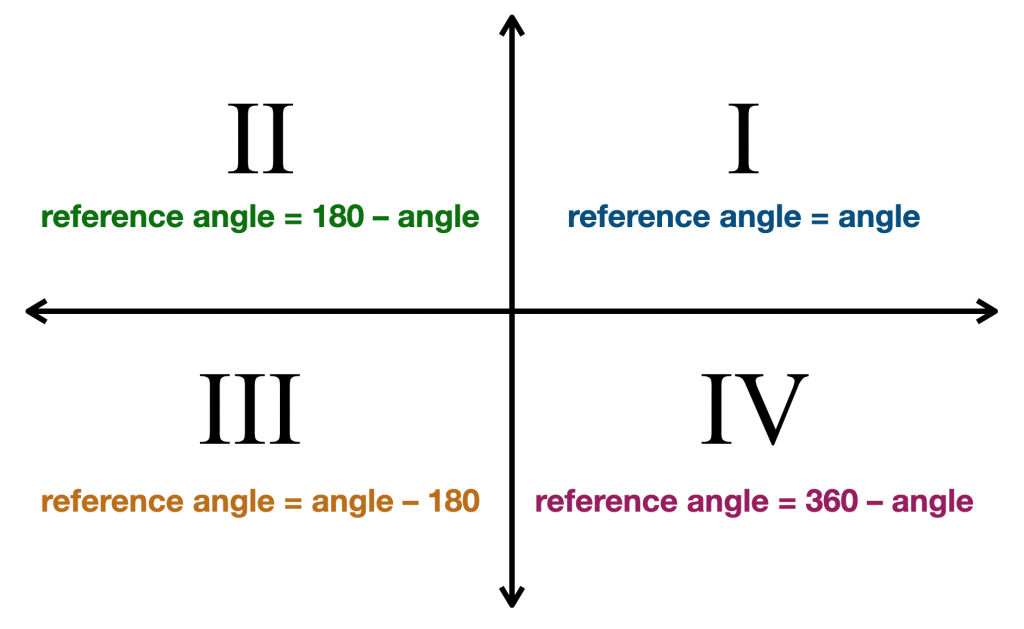
Trigonometric Ratios In Quadrants 2, 3 and 4 If the terminal arm of an angle falls in quadrants 2, 3 or 4, we use a reference angle of 6;Trigonometry (from Greek trigōnon, "triangle" and metron, "measure") is a branch of mathematics that studies relationships between side lengths and angles of triangles The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies · Our reference angle calculator is a handy tool for recalculating angles into their acute version All you have to do is simply input any positive angle into the field and this calculator will find the reference angle for you This article explains what a reference angle is, providing a reference angle definition


4 3a Trigonometric Ratios Ppt Download


Quadrant
1 θ=40D 2 160θ= D 3 θ=−3D Exercises Sketch each of the following angles in standard position (Do not use a protractor;Additional Mathematics Secondary 3/4 Trigonometry Four Quadrants Demo VideoPresented by Mr Chok, Master Maths Tutor of KentRidge Tuition CentreProduced byQuadrants in Trigonometry The signs of the three basic trigonometric functions, sin, cos, and tan, vary based on which quadrant they are in The sign of each trigonometric function in each quadrant can be determined using the signs of the coordinates along with basic trigonometric



If Cos X 2 12 13 And X Lies In Quadrant I Find The Values Of I Sin Youtube


Important Trigonometric Identiti
Quadrant II (90˚ < θ < 180˚) In the following diagram, θ is in the second quadrant The reference angle, α = 180˚ – θ Sine is positive whereas cosine and tangent are negative Quadrant III (180˚ < θ < 270˚) In the following diagram, θ is in the third quadrant The reference angle, α = θ – 180˚You can maybe abbreviate "Quadrant" as "Q", but don't completely omit it;In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others
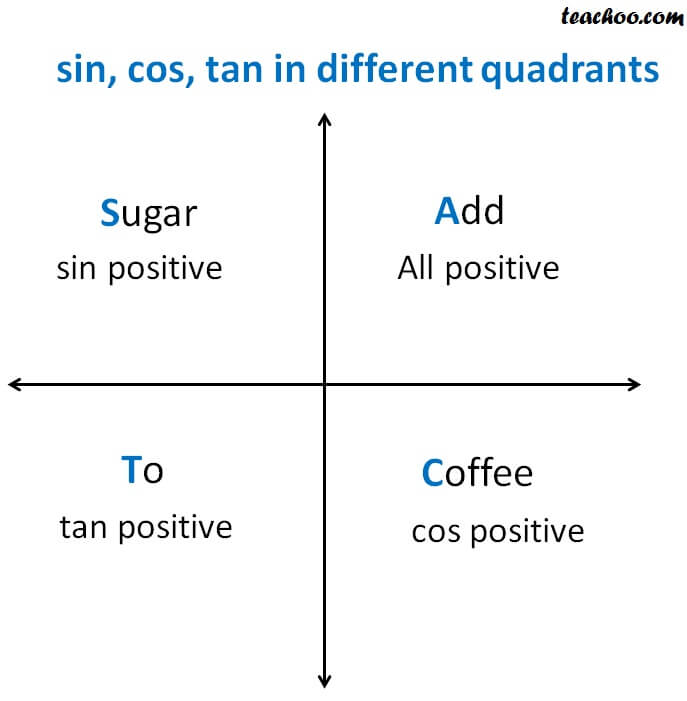


Signs Of Sin Cos Tan In Different Quadrants Finding Value Of Trign
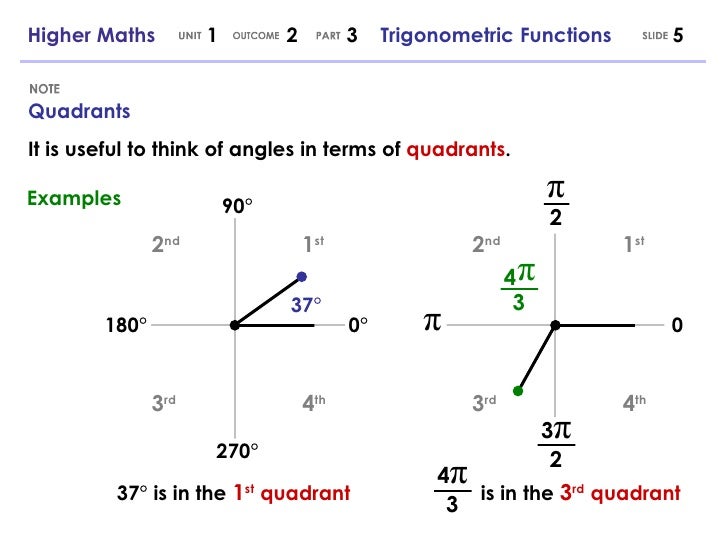


Higher Maths 1 2 3 Trigonometric Functions
Trigonometry Examples Popular Problems Trigonometry Find the Other Trig Values in Quadrant I cos(t)=3/5 Use the definition of cosine to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the valuesAngles in the different quadrants By convention, positive angles are measured in the anticlockwise direction starting from the positive \(x\) axis \(a\) and \(b\) will range between \(1\) and \(1\) depending on quadrantSection 43 Exercises 1 The 450° angle lies on the positive–y axis (450°360°=90°), while the others are all coterminal in Quadrant II 2 The angle lies in Quadrant I , while the others are all coterminal in Quadrant IV In #3–12, recall that the distance from the origin is r= 3 sin ¨= , cos ¨=– , tan ¨=–2;


Cast Rule Mathonline
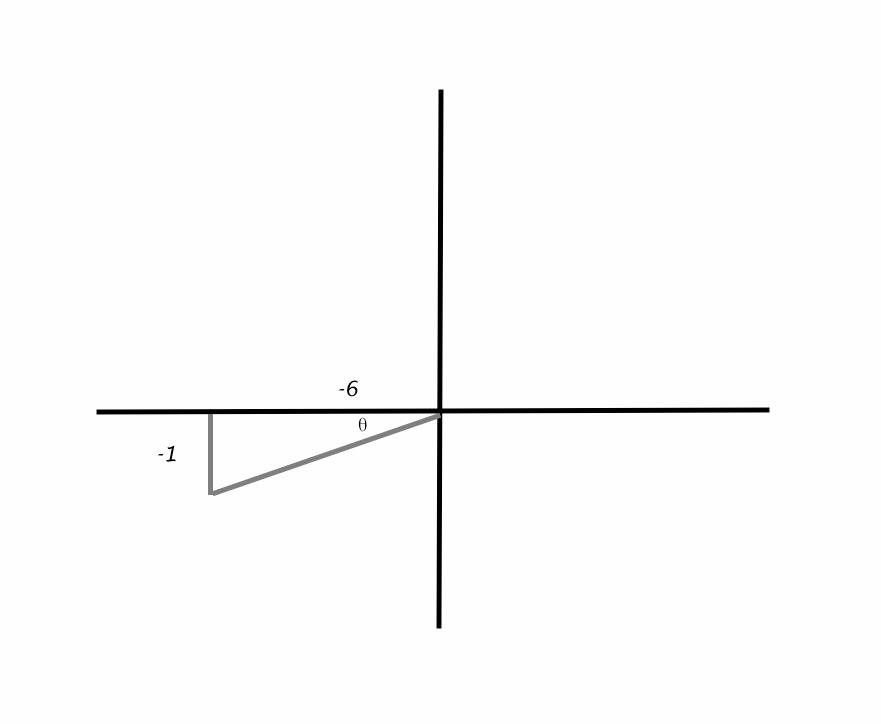


The Terminal Side Of 8 Lies On A Given Line In The Specified Quadrant Find The Values Of The Six Trigonometric Functions Of 8 By Finding A Point On The Line Line
Examples Based on Signs of Trigonometric Ratios Example – 01 State the signs of following Trigonometric Ratios (Functions) sin 675 o sin 675 o = sin (360 o 315 o) = sin (315 o) = sin (270 o 45 o) Thus the angle 675 o lies in the fourth quadrant, where sin function is negative Hence sin 675 o is negative sin 159 o sin 159 o = sin (90 o 69 o) Thus the angle 159 o lies in secondJust draw a brief sketch) 1 1θ= D 2 45θ=− D 3 130θ=− D 4 θ=270D θ=−90D 6 θ=750D x y θ Notice that the terminal sides in examples 1 and 3 are in the same position, but they do not represent the same angle (because
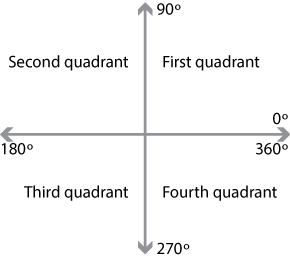


Content The Four Quadrants
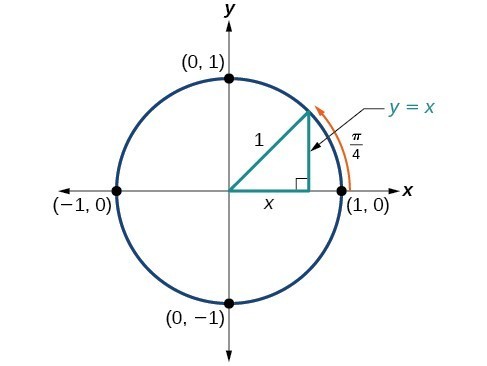


Unit Circle Sine And Cosine Functions Precalculus Ii


5 2 Unit Circle Sine And Cosine Functions Mathematics Libretexts



4 3a Trigonometric Ratios Ppt Download


Mm12 Chapter 14 The Unit Circle Combined Activity Builder By Desmos
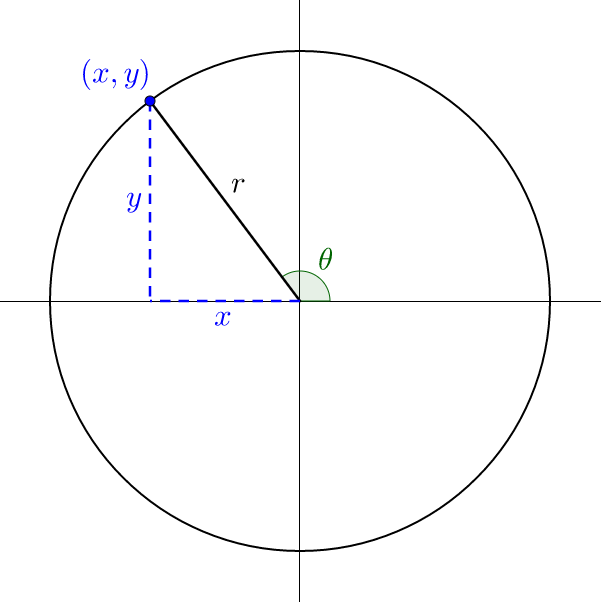


4 05 Trigonometric Functions Of Any Angle



Rotation Angle Trigonometry Pi Weeka For The Follo Chegg Com


Reference Angle Calculator Pi Day


Applying Trig Functions To Angles Of Rotation Trigonometry Socratic



Trig Unit Circle Review Article Khan Academy



Ex Find Trig Function Values Given The Cosine Value And Quadrant Youtube


If Tan 8 Is Positive And Sin 8 Is Negative In Which Quadrant Does 8 Lie Quora


The Trigonometric Ratios Of Angl


Biomath Trigonometric Functions



Graph Of Y Tan X Video Trigonometry Khan Academy
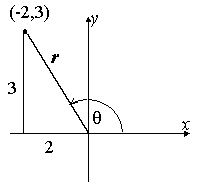


5 Signs Of The Trigonometric Functions


Domain And Range Of Inverse Trigonometric Functions



Defining Ratios In The Cartesian Plane Trigonometry Siyavula



What Trig Functions Are Positive In Which Quadrants Socratic


Cast Rule Mathonline
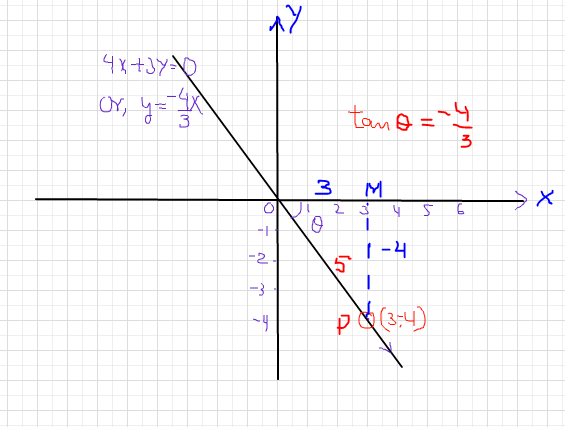


The Terminal Side Of Theta Lies On The Line 4x 3y 0 In Quadrant Iv How Do You Find The Values Of The Six Trigonometric Functions By Finding A Point On The Line
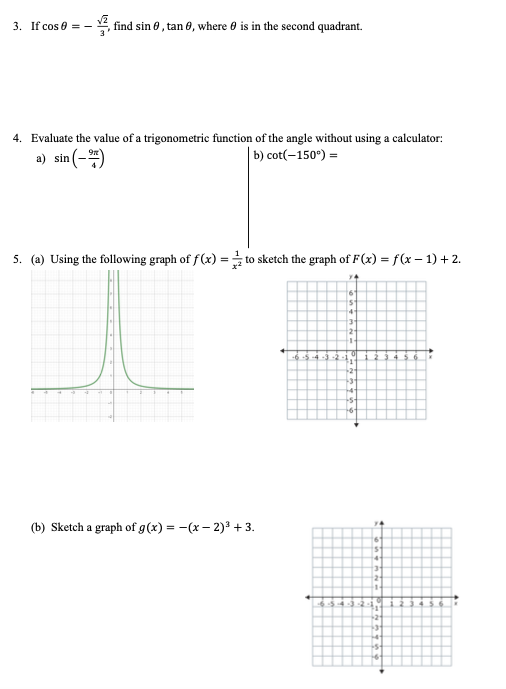


Solved 3 If Cos Find Sin 8 Tan 6 Where Is In The Chegg Com



Trigonometry
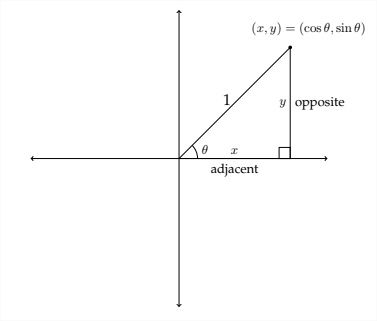


2 1 Trigonometric Functions Of Non Acute Angles Mathematics Libretexts
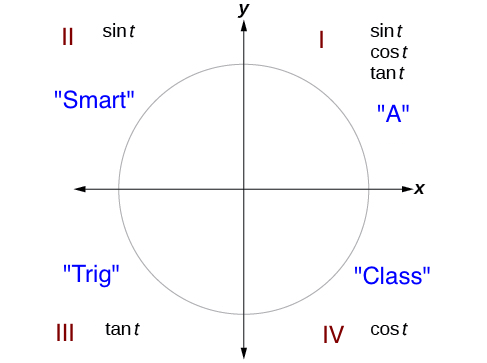


Trigonometric Functions And The Unit Circle Boundless Algebra



High School Trigonometry Relating Trigonometric Functions Wikibooks Open Books For An Open World



Graph Quadrants Examples Definition Video Lesson Transcript Study Com
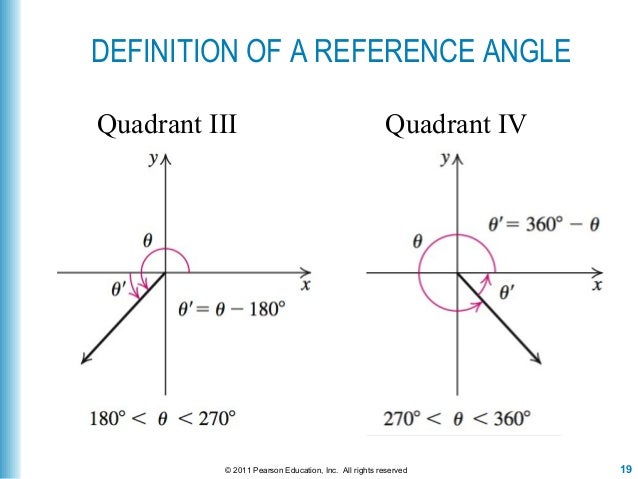


Lecture 14 Section 5 3 Trig Fcts Of Any Angle
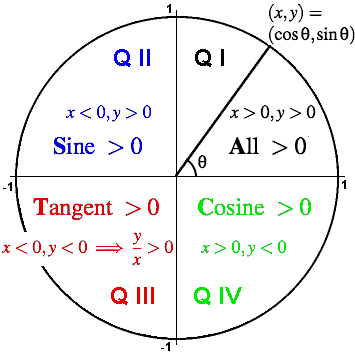


Trigonometry Facts The Amazing Unit Circle
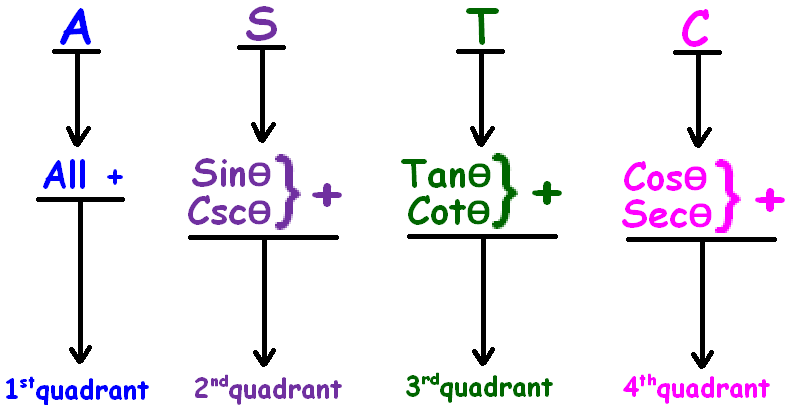


Astc Formula
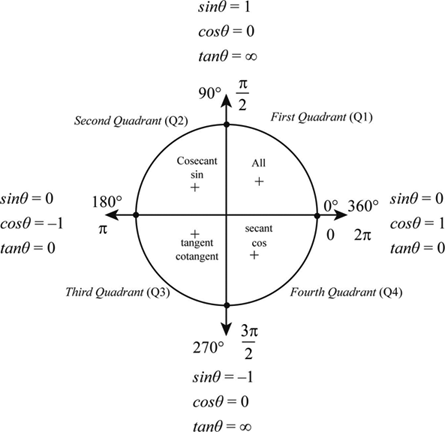


Definition Of Trigonometric Functions Of Quadrantal Angles Chegg Com



Chapter 4 Title Page 4 Lesson 3 Primary Trig Ratios Special Angles 2 A To Find



Solved The Point P X Y Is On The Unit Circle In Quadran Chegg Com



Chapter 6 Trigonometry Section 6 4 Trigonometric Functions


Solution One Of The Primary Trigonometric Ratios For An Angle Is Given As Well As The Quadrant That The Terminal Arm Lies In Determine The Other Two Primary Trigonometric Ratios A Sin
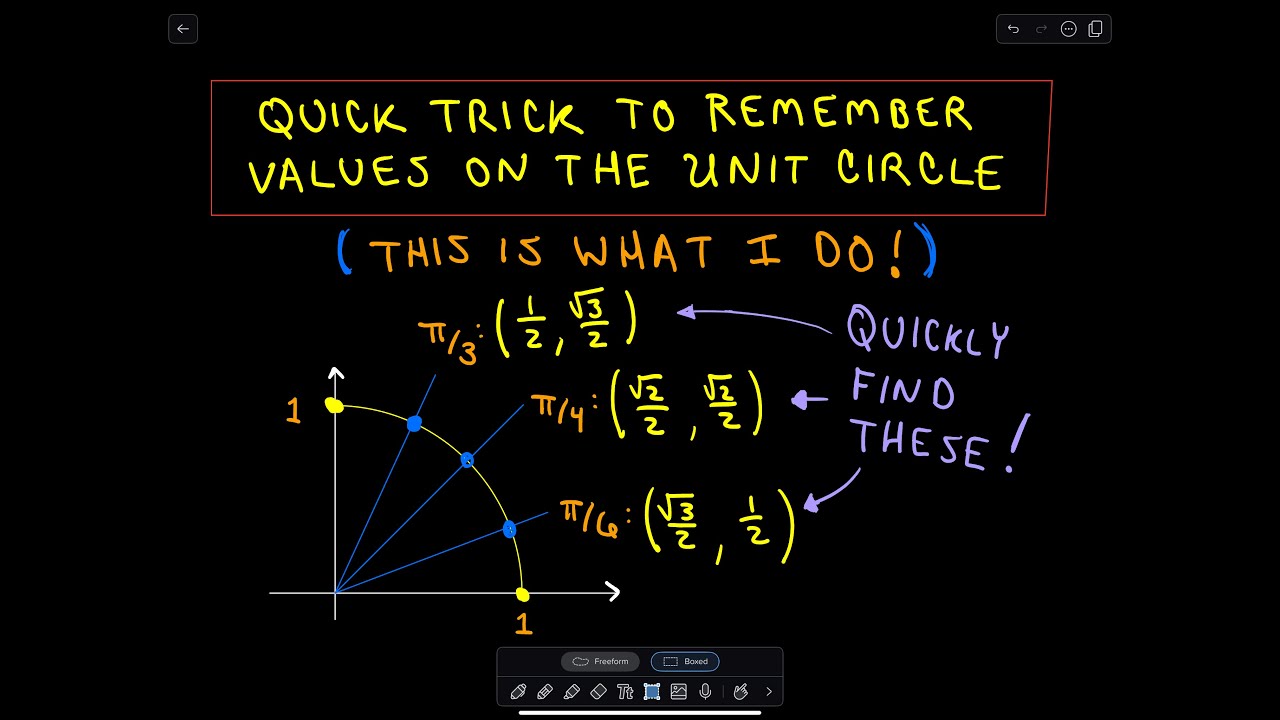


A Trick To Remember Values On The Unit Circle Youtube



Activity 4 2 Trig Ratios Of Any Angles
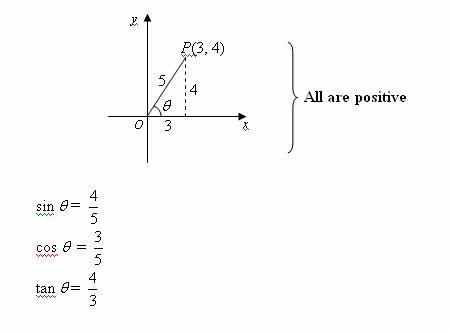


Trigonometric Ratios Solutions Examples Videos
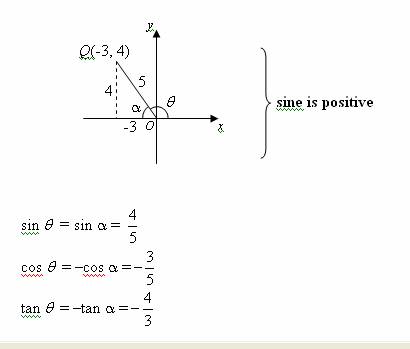


Trigonometric Ratios Solutions Examples Videos



Signs Of Sin Cos Tan In Different Quadrants Finding Value Of Trign
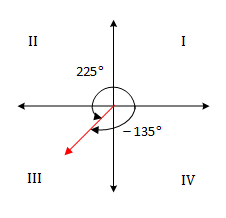


Trigonometry Quadrants And Quadrantal Angles



Given Sin A 2 5 And In Quadrant Ii Find 5 Trig Function Values Youtube


The Trigonometry Functions


Trigonometric Functions Of A General Angle
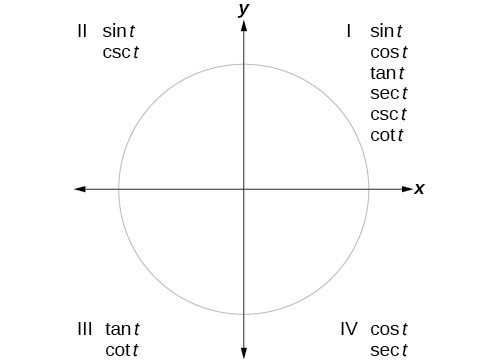


Section 4 4 Reference Angles Precalculus
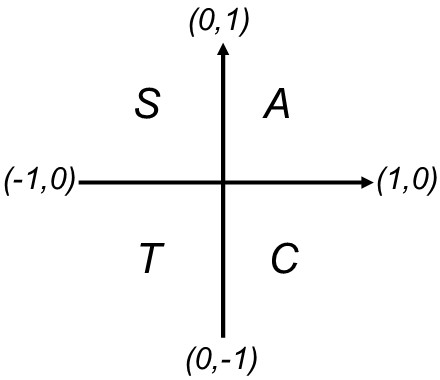


Math 1za3 Trigonometric Functions
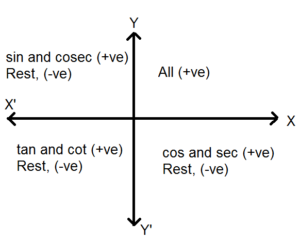


Signs Of Trigonometric Ratios In Diffrent Quadrants Formed Due To Axes



Trigonometric Functions And The Unit Circle Boundless Algebra



Astc Formula


Trigonometry Trigonometric Functions Functions In Quadrants Sparknotes
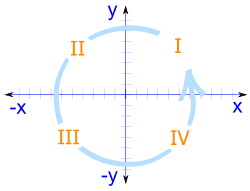


Sine Cosine And Tangent In Four Quadrants
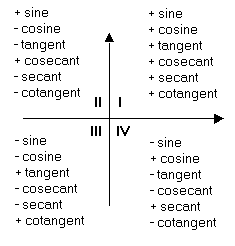


What Trig Functions Are Negative In Quadrant 2 Socratic
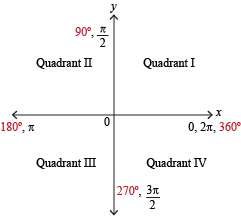


Quadrants
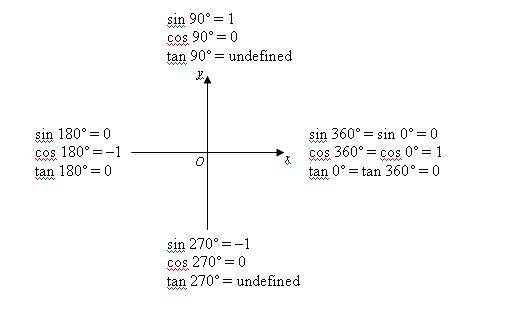


Trigonometric Ratios Solutions Examples Videos
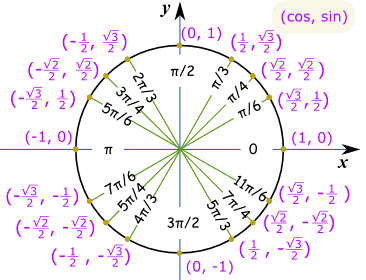


Easy Way Of Memorizing Values Of Sine Cosine And Tangent Mathematics Stack Exchange
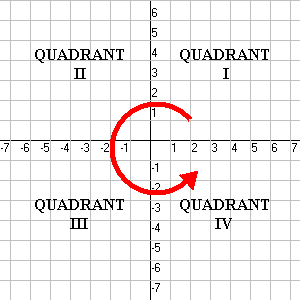


Quadrants


Unit Circle Trigonometry
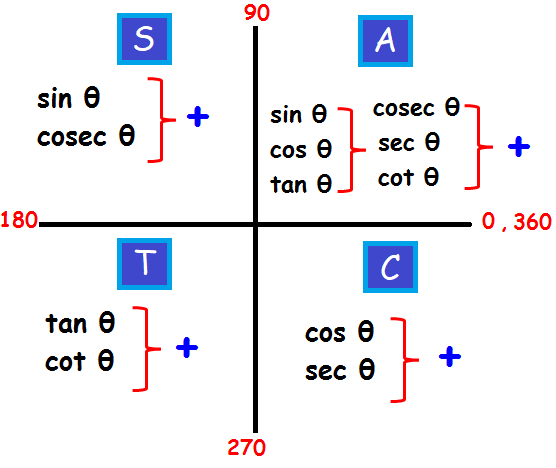


Trigonometry Quadrant Formulas



Quadrant Plane Geometry Wikipedia
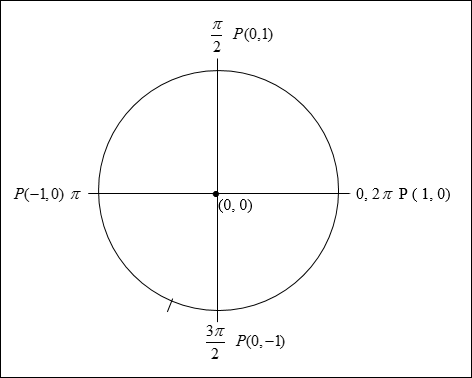


Circular Trigonometry



Trigonometric Functions Justin Skycak



Domain Range And Signs Of Trigonometric Functions Read Trigonometry Ck 12 Foundation
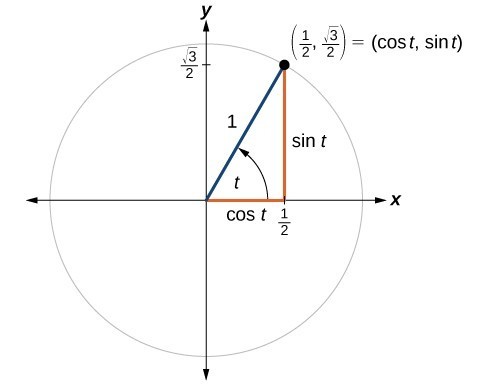


Unit Circle Sine And Cosine Functions Precalculus Ii
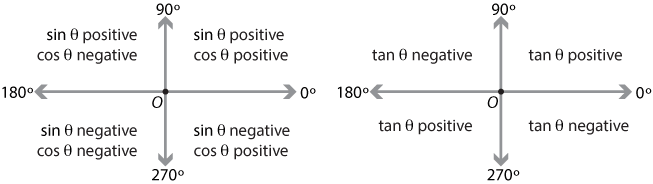


Content The Four Quadrants


Unit Circle Trigonometry



If Tan Theta 3 4 And Theta Is Not In First Quadrant Then Sin Pi 2 Theta Cot Pi Theta Youtube



Unit Circle Memorizing The First Quadrant Video Lesson Transcript Study Com


Special Angles In The Unit Circle



Ex 3 2 3 If Cot X 3 5 Find Values Of Other Trigonometric



0 件のコメント:
コメントを投稿